【小1算数】くり上がりのある足し算の計算方法から応用できる思考まで
Contents
今回のブログは、「くりあがりのある足し算」の答えの出し方についてです。
新年度まであと1ヶ月と少しとなりました。
新1年生になる皆さんの中には、
算数の学習を進める中で、「くり上がりのある足し算」の学習に取り組もうとしている方もいます。
ただ、まだ1年生になっていないので、教科書がお手元にありません。
そうした中で、どうやって理解をしていけば良いか、と戸惑っている子やお父さま、お母さまもいらっしゃるかもしれません。
そこで、今回は、
「くり上がりのある足し算」の解き方について、入学を前に紹介します。
あわせて、教科書で教えられている「くり上がりのたし算」の計算方法が、
小学校2年生以降の学習においても活かしていける思考であることを確認していきます。
くり上がりのたし算は「10のかたまり」を作ることで計算する。
今回は、「8+5=」という計算の解き方を例にして考えてみましょう。
計算の結果が10を超える「くり上がり」の計算は、
それまでの、答えが10以下の足し算と違って、「指を使って考える」ということができません。
そこで、次に考えられる計算方法が、いわゆる「数え足し」のやり方です。
8から、数を1個ずつ数えながら、5回数え上げていきます。
(8から)「9、10、11、12、13」
この考え方を数式で表すと、
8+5
=8+(1+1+1+1+1)
=(8+1)+1+1+1+1
=(9+1)+1+1+1
=(10+1)+1+1
=(11+1)+1
=12+1
=13
という順番で計算をしていっている、ということでもあります。
数え足しは、足す数が1桁くらいなら(9こ数え上げるくらいまでなら)、答えを出す方法として使えなくはないです。
ところが、2桁以上の数を足すようになると、このやり方では限界がきます。
(もちろん、そうでなくても1問における計算時間がかかりすぎてしまいます。上の計算式を見ても、計算を分解しすぎていて手間がかかる、というのがわかると思います。)
そこで、くり上がりのある計算は、
それまでに学習している、「10までの計算」を活用することで、よりスムーズに解くことができるようになります。
ステップ①:足される数(8)は、あといくつで10になるか?を考える
「あといくつ?」という表現は、
くり上がりの学習をする手前の「ひき算」の学習の際に取り組んでいます。
ただ、計算の仕方を覚えるだけでなく、
こういった「言葉の理解」をすることも、
次の学習を進めていく上で大切な知識なのです。
くり上がりの足し算は、
まずは、10個いりの箱をイメージして、先にその箱を全て埋め切ることから考えます。
(あるいは硬貨を使った計算なら、まず10円玉に両替できる1円玉10枚を集めることを考えます。)
この時に必要なのが、「あといくつで10?」という考え方なのです。
この場合、「10ー8=2」なので、
8は、あと2で10になることがわかります。
ステップ②:10を作ったあと、足す数である5が、「いくつ残っているか」を考えます。
8が、あと2で10になることがわかったら、
まず、足す数の5の中から、先に2だけ足します。
すると、足す数の5はいくつ残っているかというと、
「5−2=3」で、3だけ残っていることがわかります。
ステップ③:できた10に、残りの3を足して計算完了
この計算の方法を式で表すと、
8+5
=8+(2+3) (∵2=10−8、3=5−2)
=(8+2)+3
=10+3
=13
となります。
途中で、2回の引き算の計算を(頭の中で)していることがポイントです。
実際の計算では、
足す数の5の下に2つ線を分けて、2と3を書くことで計算をするので、
途中式を書かず、1行で計算をしていくようなやり方になります。
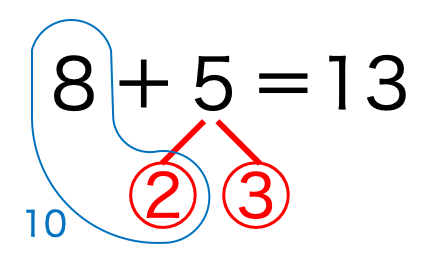
(実際の計算では、青の線や数字は書かず、赤の線と数字だけを書き加えて計算するようなやり方となります。)
足す数の5を、2と3の2つの数に分けている赤色の部分が、
「さくらんぼ」に似ていることから、
「さくらんぼ計算」などと言われています。
「さくらんぼ計算」を使って、くり上がりの計算を学習する意義
この、「さくらんぼ計算」が、
小学校1年生の「くり上がりの足し算」の計算方法として使われていることには、
いくつかメリットがあると考えています。
順に、さくらんぼ計算のメリットをみていきましょう。
メリット①:すでに学習した内容が、次のレベルの学習に活用していけるという「学びのステップ」を理解できる。
先ほど紹介したとおり、
くり上がりのあるたし算を「さくらんぼ計算」を使って解く際には、
・10から「足される数」を引く引き算(10ー□=△)
・「足す数」を、△と残りの数に分ける引き算
をすることになります。
10までの数が、「いくつといくつに分かれるか」
を、ひと通りマスターしていれば、
今まで取り組んでいなかった「答えが10を超える計算」についても、答えを出せるのです。
この、「これまでに学んだ内容を使って、次のレベルの学習を理解していく」というのが、
学びのレベルを上げていく時の、基本の姿勢ということになります。
算数学習のカリキュラムは、
たとえそれが「難しい」と感じる単元や学習内容であっても、
それまでに学んだ内容が理解できていれば、必ず理解をすることができるように作られているのです。
算数の学習を進めていく上で、
この「大前提」をおさえられていることは、
新しい学習単元の内容を、自力で理解していく上でも、非常に役に立ちます。
新しい単元であっても、それは答えがある問題であり、答えに至るまでのプロセスに必要な道具は、すべて揃っている。
そのことが判っているだけでも、「よし、これを自分で理解してやろう」という意識になりやすいものです。
メリット②:次の学習をすることが、イコールそれまでの内容の「復習」となる。
これまでに学習した内容が盛り込まれている新しい単元の学習では、
過去に学習した内容を使いこなしながら、学習を進めていくことになります。
と、いうことは、
あえて、過去の単元を「復習しよう」と思わなくても、
新しい単元の学習を進めていくことで、
勝手に、復習を繰り返していくことになるのです。
今回の「さくらんぼ計算」においては、
くり上がりのある足し算に取り組む中で、
10までの数の構成を覚えていくことも、同時に行うことができているのです。
次の単元の学習を進めていく中で、
前の単元の理解も深まっていくのです。
メリット③:さらに発展的な内容の学習にも応用できる「かたまり思考」を手に入れられる。
さくらんぼ計算は、
くり上がりのある足し算(例えば、8+5)の答えを知らない人が、
スムーズに答えを出すための計算テクニックでもあります。
ということは、
その時の考え方を応用することで、
より難しい計算問題の解き方も身につけることができるのです。
たとえば、
「89+36+11」という計算があったときに、
「89+11」を先に計算する、ということは、
「(100の)かたまりを作る」という発想があるからできることです。
同様に、
「25×28」という計算は、
25×28
=25×(4×7)
=(25×4)×7
=100×7
とすることで、
暗算だけでも正確に解けます。
いずれも、「さくらんぼ計算」と同じで、
「キリのいい数のかたまりを作る」ことで、計算をスムーズにすることができます。
のちの「計算の工夫」として学ぶような、計算をスムーズにするための考え方を、
すでに小学校1年生の時点から、学ぶことができているのです。
単なる「1桁+1桁の足し算」ですが、
それを学習する過程で、
後々の算数学習のステップアップに必要な考え方の土台を、
しっかり身につけることができるのです。
「さくらんぼ計算」は、くり上がりの計算のゴールではない。
なお、この「さくらんぼ計算」で、繰り上がりのたし算の意味を理解した後は、
「18までの数の構成を把握する」ことで、
計算のスピードが劇的に上がります。
ひと通り、「さくらんぼ計算」で答えを出すことができるようになったら、
くり上がりのある足し算についても「即答」できることを目指してみてください。
それが、そのまま、「2桁以上の足し算(筆算)」の計算に繋がっていきます。

